Answers
Answer:
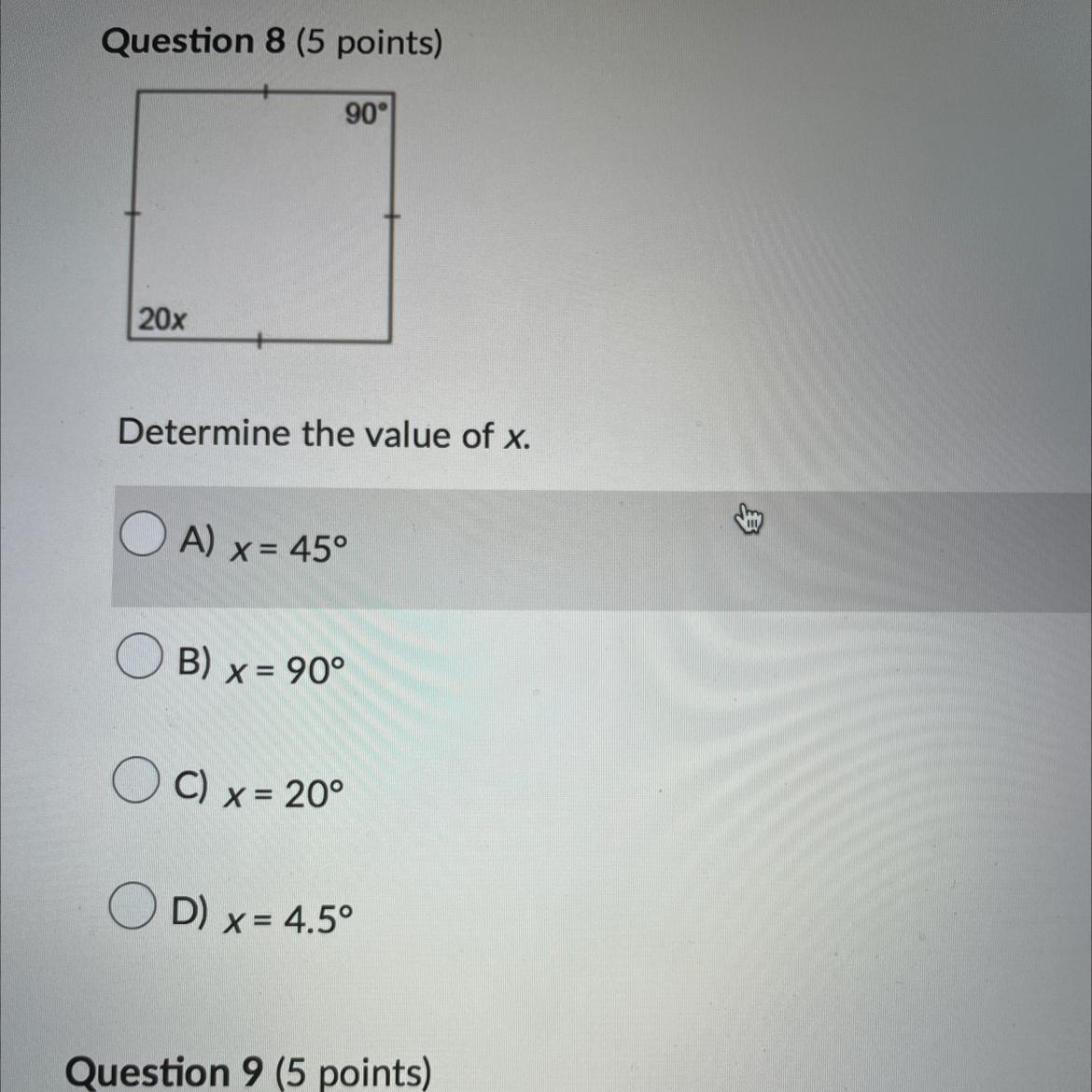
x=4.5
Step-by-step explanation:
We know that if all sides are congruent then all angles must also be congruent, therefore you can solve for x with the following equation:
[tex]20x=90[/tex]
Solve
[tex]x=4.5[/tex]
Related Questions
Kyle Records the rainfall,in inches, for four days and records the data on the line plot. Kyle then records for a fifth day,the total is 5 1/2 inches of rain. What is the total amount of rain on the fifth day?
Answers
Kyle recorded the rainfall, in inches, for four days and represented the data on a line plot. He then recorded the total rain for the fifth day, which was 5 1/2 inches. The total amount of rain on the fifth day is 5 1/2 inches.
Kyle represented the first four days' rainfall data on a line plot. Line plots express data where the number of times each value occurs is plotted against the actual values. In this case, the actual values are the amount of rainfall in inches.
Kyle recorded the rainfall for four days and represented the data on a line plot. The line plot showed the rainfall for each day, and the total amount of rain recorded was 5 inches. Kyle then recorded the total rainfall for the fifth day, which was 5 1/2 inches. Thus, the total amount of rain on the fifth day is 5 1/2 inches.
If it is represented on the line plot, the line plot will show an additional 5 1/2 inches of rainfall. This is because the line plot shows the amount of precipitation for each day. Kyle recorded the rainfall, in inches, for four days and represented the data on a line plot. He then recorded the total rain for the fifth day, which was 5 1/2 inches. The total amount of rain on the fifth day is 5 1/2 inches.
To know more about the line plot, visit:
brainly.com/question/16321364
#SPJ11
a normal population has a mean of $95 and standard deviation of $14. you select random samples of 50.Required: a. Apply the central limit theorem to describe the sampling distribution of the sample mean with n= 50. What condition is necessary to apply the central limit theorem? b. What is the standard error of the sampling distribution of sample means? (Round your answer to 2 decimal places.) c. What is the probability that a sample mean is less than $94? (Round z-value to 2 decimal places and final answer to 4 decimal places.) d. What is the probability that a sample mean is between $94 and $96? (Round z-value to 2 decimal places and final answer to 4 decimal places.)e. What is the probability that a sample mean is between $96 and $97? (Round z-value to 2 decimal places and final answer to 4 decimal places.)f. What is the probability that the sampling error ( X - u) would be $1.50 or less? (Round z-value to 2 decimal places and final answer to 4 decimal places.)
Answers
156.05 is respectfully the correct answer but 4 decimal place - 156.1
Using a standard normal distribution table, the probability that z is less than 0.76 is approximately 0.7764.
According to the central limit theorem, the sampling distribution of the sample mean is approximately normal with a mean equal to the population mean, which is $95 in this case, and a standard deviation equal to the population standard deviation divided by the square root of the sample size, which is $14/sqrt(50) ≈ $1.98. The central limit theorem applies when the sample size is large enough, typically n ≥ 30, and the population is not strongly skewed.
The standard error of the sampling distribution of sample means is equal to the standard deviation of the population divided by the square root of the sample size, which is $14/sqrt(50) ≈ $1.98.
To find the probability that a sample mean is less than $94, we need to standardize the sample mean using the formula z = (X - u) / SE, where X is the sample mean, u is the population mean, and SE is the standard error of the sampling distribution. Thus, z = (94 - 95) / 1.98 ≈ -0.51. Using a standard normal distribution table, the probability that z is less than -0.51 is approximately 0.3043.
To find the probability that a sample mean is between $94 and $96, we need to standardize both values and find the area between them under the standard normal distribution curve. Using the same formula as in (c), we get z1 = (94 - 95) / 1.98 ≈ -0.51 and z2 = (96 - 95) / 1.98 ≈ 0.51. Using a standard normal distribution table, the probability that z is between -0.51 and 0.51 is approximately 0.4641.
To find the probability that a sample mean is between $96 and $97, we follow the same steps as in (d) and get z1 = (96 - 95) / 1.98 ≈ 0.51 and z2 = (97 - 95) / 1.98 ≈ 1.01. Using a standard normal distribution table, the probability that z is between 0.51 and 1.01 is approximately 0.1554.
To find the probability that the sampling error ( X - u) would be $1.50 or less, we need to standardize this value and find the area to the left of it under the standard normal distribution curve. Thus, z = (1.5) / 1.98 ≈ 0.76. Using a standard normal distribution table, the probability that z is less than 0.76 is approximately 0.7764.
To learn more about Standard normal distribution :
https://brainly.com/question/4079902
#SPJ11
A man buys two cycles for a total cost of Rs. 900. By selling one for 4/5 of its cost and other for 5/4 of its cost, he makes a profit of Rs. 90 on whole transaction. Find the cost price of lower priced cycle
Answers
the cost price of the lower priced cycle is Rs. 130.. Then the cost price of the other cycle would be (900 - x), since the total cost of the two cycles is Rs. 900.
The man sells one cycle for 4/5 of its cost, which means he earns 4/5 of the cost price as revenue. So, the revenue earned by selling the first cycle would be (4/5)x. Similarly, the revenue earned by selling the other cycle would be (5/4)(900 - x) = (1125 - 5/4x).
The total revenue earned by selling both cycles is (4/5)x + (1125 - 5/4x) = (500 + 15/4x). The profit made on the transaction is Rs. 90. So, we have:
Total revenue - Total cost = Profit
(500 + 15/4x) - 900 = 90
Simplifying the equation, we get:
15/4x - 400 = 90
15/4x = 490
x = 130
Therefore, the cost price of the lower priced cycle is Rs. 130.
to learn more about price click here:brainly.com/question/19091385
#SPJ11
use logarithmic differentiation to determine y′ for the equation y=(x 9)(x 3)(x 2)(x 6). write your answer in terms of x only.
Answers
Using logarithmic differentiation, the derivative of y with respect to x is given by y' is (x+9)(x+3)(x+2) + (x+9)(x+3)(x+6) + (x+9)(x+2)(x+6) + (x+3)(x+2)(x+6)
We have y=(x+9)(x+3)(x+2)(x+6).
Taking the natural logarithm of both sides, we get
ln(y) = ln[(x+9)(x+3)(x+2)(x+6)]
Using the properties of logarithms, we can simplify this to:
ln(y) = ln(x+9) + ln(x+3) + ln(x+2) + ln(x+6)
Now, we can implicitly differentiate both sides with respect to x
1/y * y' = 1/(x+9) + 1/(x+3) + 1/(x+2) + 1/(x+6)
Multiplying both sides by y, we get
y' = y * [1/(x+9) + 1/(x+3) + 1/(x+2) + 1/(x+6)]
Substituting y=(x+9)(x+3)(x+2)(x+6), we get
y' = (x+9)(x+3)(x+2)(x+6) * [1/(x+9) + 1/(x+3) + 1/(x+2) + 1/(x+6)]
Simplifying this expression, we get
y' = (x+9)(x+3)(x+2) + (x+9)(x+3)(x+6) + (x+9)(x+2)(x+6) + (x+3)(x+2)(x+6)
Thus, y' = (x+9)(x+3)(x+2) + (x+9)(x+3)(x+6) + (x+9)(x+2)(x+6) + (x+3)(x+2)(x+6)
To know more about logarithmic differentiation:
https://brainly.com/question/32030515
#SPJ4
--The given question is incomplete, the complete question is given
" use logarithmic differentiation to determine y′ for the equation y=(x+9)(x+3)(x+2)(x+6). write your answer in terms of x only."--
The volume of a sphere is given by the equation V=43πr3. If a basketball has a volume of approximately 381. 7 in. 3, what is the approximate diameter of the basketball? Use 3. 14 as an approximation of π. Is it 4. 5 in, 9. 0 in, 10. 0 in, 20. 0 in
Answers
the approximate diameter of the basketball is 9.0 inches.
To find the diameter of the basketball, we can use the formula for the volume of a sphere:
V = (4/3)πr^3
Given that the volume of the basketball is approximately 381.7 in^3, we can set up the equation:
381.7 = (4/3)(3.14)(r^3)
Simplifying the equation:
381.7 = 4.1867r^3
Dividing both sides by 4.1867:
r^3 = 91.288
Taking the cube root of both sides to solve for r:
r ≈ 4.5
The radius of the basketball is approximately 4.5 inches. To find the diameter, we double the radius:
d ≈ 2r ≈ 2(4.5) ≈ 9.0
To know more about equation visit:
brainly.com/question/29538993
#SPJ11
Please Please Please help!
The dot plots below show the ages of students belonging to two groups of salsa classes:
A dot plot shows two divisions labeled Group A and Group B. The horizontal axis is labeled as Age of Salsa Students in years. Group A shows 3 dots at 5, 4 dots at 10, 6 dots at 17, 4 dots at 24, and 3 dots at 28. Group B shows 6 dots at 7, 3 dots at 10, 4 dots at 14, 5 dots at 17, and 2 dots at 22.
Based on visual inspection, which group most likely has a lower mean age of salsa students? Explain your answer using two or three sentences. Make sure to use facts to support your answer. (10 points)
Answers
Based on visual inspection, Group A most likely has a lower mean age of salsa students.
How to explain the meanUpon visually inspecting the dot plots, it is evident that Group A has a larger number of dots clustered around the lower ages (5 and 10) compared to Group B. This indicates that Group A likely has a higher frequency of younger students. In contrast, Group B has a higher concentration of dots at higher ages (17 and 22), suggesting a higher frequency of older students.
This is because Group A has a greater concentration of dots towards the lower ages, such as 5 and 10, while Group B has a greater concentration towards the higher ages, such as 17 and 22. This suggests that the average age of students in Group A is likely to be lower than that of Group B.
Learn more about mean on
https://brainly.com/question/1136789
#SPJ1
A normal population has mean = 58 and standard deviation 0 = 9. what is the 88th percentile of the population? Use the TI-84 Plus calculator. Round the answer to at least one decimal place, The 88th percentile of the population is
Answers
The 88th percentile of the population is 68.5, rounded to one decimal place.
To find the 88th percentile of a normal distribution with mean 58 and standard deviation 9, we can use the TI-84 Plus calculator as follows:
Press the STAT button and select the "invNorm" function.Enter 0.88 as the area value and press the ENTER button.Enter 58 as the mean value and 9 as the standard deviation value, separated by a comma.Press the ENTER button to calculate the result.The result is approximately 68.5. Therefore, the 88th percentile of the population is 68.5, rounded to one decimal place.
To know more about standard deviation refer to-
https://brainly.com/question/23907081
#SPJ11
A mean average of 60 on 7 exams is needed to pass a course. On her first 6 exams, Sheryl received grades of 47 comma 67 comma 74 comma 62 comma 66 and 76. What grade must she receive on her last exam to pass the course?
Answers
The answer is that Sheryl needs to receive a grade of at least 90 on her last exam to pass the course with a mean average of 60 on all 7 exams.
To find out what grade Sheryl needs on her last exam, we first need to calculate the total score she has received on her first 6 exams.
47 + 67 + 74 + 62 + 66 + 76 = 392
We then need to calculate what score she needs on her 7th and final exam to achieve a mean average of 60 for all 7 exams.
To do this, we can use the formula:
(mean average) x (number of exams) = total score
Substituting in the values we have:
60 x 7 = 420
We already know that Sheryl has scored a total of 392 on her first 6 exams. Therefore, we can calculate the score she needs on her final exam:
420 - 392 = 28
This means that Sheryl needs to score an additional 28 points on her last exam to achieve a mean average of 60 for all 7 exams.
However, we also need to keep in mind that the maximum score on an exam is usually 100. Therefore, if Sheryl wants to pass the course, she needs to score a grade of at least 90 on her final exam.
Sheryl needs to score a grade of at least 90 on her last exam to pass the course with a mean average of 60 on all 7 exams, based on the calculations of her previous scores and the maximum score on an exam.
To know more about average visit:
brainly.com/question/24057012
#SPJ11
Let V be a finite-dimensional inner product space. Suppose TEL(V). (a) Prove that T and T* have the same singular values. (b) Prove that dim range T equals the number of nonzero singular values of T.
Answers
a. The singular values of T and T* are the square roots of the same set of eigenvalues, and so they are equal.
b. The range of T is spanned by the vectors {u1, u2, ..., un}.
Moreover, since[tex]T(vi) = \sqrt{( \lambda i)u_i, }[/tex] we see that the dimension of the range of T is the same as the number of nonzero singular values of T, which is the number of positive square roots of the eigenvalues of T*T.
(a) To prove that T and T* have the same singular values, we first note that the singular values of T and T* are the square roots of the eigenvalues of TT and TT*, respectively.
This is because if we diagonalize TT and TT*, the singular values will be the square roots of the diagonal entries.
Now, since V is finite-dimensional, we know that TT and TT* are both self-adjoint and have the same eigenvalues. This is because the eigenvalues of TT and TT* are the same as the eigenvalues of TTT and TTT*, respectively, and these matrices are similar to each other (they have the same Jordan canonical form) because T and T* have the same characteristic polynomial.
Therefore, the singular values of T and T* are the square roots of the same set of eigenvalues, and so they are equal.
(b) We know that the singular values of T are the square roots of the eigenvalues of TT.
Since TT is self-adjoint, it can be diagonalized with respect to an orthonormal basis of V. Let {v1, v2, ..., vn} be an orthonormal basis of eigenvectors of T*T with corresponding eigenvalues λ1, λ2, ..., λn.
Then, we have:
[tex]T(vi) = \sqrt{(\lambda i)u_i}[/tex]
where [tex]u_i = T(vi) / \sqrt{(\lambda i) }[/tex] is a unit vector.
Therefore, the range of T is spanned by the vectors {u1, u2, ..., un}. Moreover, since[tex]T(vi) = \sqrt{( \lambda i)u_i, }[/tex] we see that the dimension of the range of T is the same as the number of nonzero singular values of T, which is the number of positive square roots of the eigenvalues of T*T.
Hence, we have shown that the dimension of the range of T is equal to the number of nonzero singular values of T.
For similar question on singular values.
https://brainly.com/question/30480116
#SPJ11
evaluate the line integral over the curve c: x=sin(t), y=cos(t), 0≤t≤π ∫c(3x−2y)ds
Answers
The line integral over the curve c of the function f(x,y) = 3x - 2y is 6.
To evaluate the line integral of the given function over the curve c, we need to parameterize the curve and express the function in terms of the parameter.
The curve c is given by x = sin(t), y = cos(t) for 0 ≤ t ≤ π, which is the top half of the unit circle. To parameterize the curve, we can use the following vector function:
r(t) = (sin(t), cos(t)), 0 ≤ t ≤ π
Then the line integral of the function f(x,y) = 3x - 2y over the curve c can be expressed as:
∫c f(x,y) ds = ∫π₀ (3sin(t) - 2cos(t)) ||r'(t)|| dt
where ||r'(t)|| is the magnitude of the derivative of r(t) with respect to t, which is:
||r'(t)|| = √(cos²(t) + sin²(t)) = 1
Substituting this value, we get:
∫c f(x,y) ds = ∫π₀ (3sin(t) - 2cos(t)) dt
Now, we can integrate the function with respect to t:
∫π₀ (3sin(t) - 2cos(t)) dt = [-3cos(t) - 2sin(t)]π₀
Substituting the limits of integration, we get:
∫c f(x,y) ds = [-3cos(π) - 2sin(π)] - [-3cos(0) - 2sin(0)]= (3 + 0) - (-3 - 0) = 6.
For such more questions on line integral:
https://brainly.com/question/28381095
#SPJ11
The intersection of f(x,y) = 3x - 2y on curve c is 6. To evaluate the system of a function on curve c, we need to evaluate the curve and represent the following discordant activities.
The curve c is given by x = sin(t), y = cos(t), where 0 ≤ t ≤ π, this is a semicircle. We can use the following vector function to measure the curve:
r(t) = (sin(t), cos(t)), 0 ≤ t ≤ π
So the function f(x, y) = 3x - 2y on the curve c it can be represented as:
∫c f(x,y) ds = ∫π₀ (3sin(t) - 2cos(t)) r'(t)dt
where r'(t) is the magnitude of the derivative of r(t) with respect to t, for example:
r'(t) = √(cos²(t) + sin²(t)) = 1
This substituting the value we get:
∫c f(x,y) ds = ∫π₀ (3sin(t) - 2cos(t)) dt
Now we can integrate the function t (∫π₀ (3sin(t)) ) - 2cos(t)) t) - 2cos(t)) dt = [-3cos(t) - 2sin(t)]π₀
Substitution at the limit of our shares :
∫c f(x,y) ds = [-3cos( π ) - 2sin(π)] - [-3cos(0) - 2sin(0)] = (3 + 0) - (-3 - 0) = 6.
Learn more about Curve:
brainly.com/question/28793630
#SPJ11
Consider the following limit of Riemann sums of a function f on [a,b]. Identify f and express the limit as a definite integral. lim Δ→0
∑ k=1
n
x k
∗
tan 2
x k
∗
Δx k
;[1,2] The limit, expressed as a definite integral, is (Simplify your answers.)
Answers
To identify the function f and express the given limit as a definite integral, we can observe the Riemann sum expression and recognize its similarity to the definition of the definite integral. Answer : ∫[1,2] x * tan^2(x) dx.
In the given expression, we have the Riemann sum:
∑ k=1^n x_k * tan^2(x_k) * Δx_k
To express this limit as a definite integral, we recognize that the function f(x) = x * tan^2(x) is being approximated by the Riemann sum.
We can rewrite the Riemann sum as:
∑ k=1^n f(x_k) * Δx_k
Now, we can see that the function f(x) = x * tan^2(x) and the interval [a, b] are given. In this case, a = 1 and b = 2.
To express the given limit as a definite integral, we take the limit as Δx_k approaches zero and rewrite the Riemann sum as the definite integral:
lim Δx_k→0 ∑ k=1^n f(x_k) * Δx_k
This limit can be written as:
∫[a,b] f(x) dx
Substituting the values of a and b, we have:
∫[1,2] x * tan^2(x) dx
Therefore, the limit expressed as a definite integral is ∫[1,2] x * tan^2(x) dx.
Learn more about Riemann sum: brainly.com/question/30404402
#SPJ11
List all the permutations of {a, b,c}.
Answers
Here is a list of all the permutations of the set {a, b, c}. A permutation is an arrangement of elements in a specific order. Since there are three elements in this set, there will be a total of 3! (3 factorial) permutations, which is 3 × 2 × 1 = 6 permutations. Here they are:
1. abc
2. acb
3. bac
4. bca
5. cab
6. cba
These are all the possible permutations of the set {a, b, c}.
To know more about permutations, visit:
https://brainly.com/question/30649574
#SPJ11
The normal line to a graph of a function f at a point (c, f(c)) is the line through (c, f(c)) perpendicular to the tangent line to the graph of f at (c, f(c)). See the figure. If f is a function whose derivative at c is f
′
(
c
)
≠
0
,
the slope of the normal line to the graph of f at (c, f(c)) is −
1
f
′
(
c
)
.
Then an equation of the normal line to the graph of f at (c, f(c)) is y
−
f
(
c
)
=
−
1
f
′
(
c
)
(
x
−
c
)
.
Find the slope of the normal line to the graph of the function at the indicated point.
f
(
x
)
=
4
x
2
+
2
a
t
(
1
,
6
)
Answers
The slope of the normal line to the graph of f(x)=4x^2+2 at (1,6) is -8.
The derivative of f(x) is f'(x) = 8x, so f'(1) = 8. Therefore, the slope of the tangent line to the graph of f(x) at (1,6) is f'(1) = 8. The slope of the normal line to the graph of f(x) at (1,6) is then -1/f'(1) = -1/8.
Using the point-slope form of a line, the equation of the normal line to the graph of f(x) at (1,6) is y-6 = (-1/8)(x-1). Simplifying, we get y = (-1/8)x + 49/8. Therefore, the slope of the normal line to the graph of f(x) at (1,6) is -8.
For more questions like Slope click the link below:
https://brainly.com/question/360544
#SPJ11
in how many ways can 10 balls be selected if at least one red ball, at least two blue balls, and at least three green balls must be selected?
Answers
There are 12,600 ways to choose 10 balls satisfying the given conditions of at least one red ball, at least two blue balls, and at least three green balls.
To calculate the number of ways to select the balls, we can use the concept of combinations.
Let's break down the selection criteria:
At least one red ball: This means we can select 1, 2, 3, 4, 5, 6, 7, 8, 9, or 10 red balls.
At least two blue balls: This means we can select 2, 3, 4, 5, 6, 7, 8, 9, or 10 blue balls.
At least three green balls: This means we can select 3, 4, 5, 6, 7, 8, 9, or 10 green balls.
To find the total number of ways to select the balls, we need to consider all possible combinations of selecting the specified number of balls from each color category. We can calculate this by summing up the combinations for each case:
Number of ways = C(1, 10) × C(2, 9) × C(3, 7) = 10 × 36 × 35 = 12,600.
Therefore, there are 12,600 ways to select 10 balls satisfying the given conditions of at least one red ball, at least two blue balls, and at least three green balls.
You can learn more about combinations at
https://brainly.com/question/28065038
#SPJ11
Suppose Diane and Jack are each attempting to use a simulation to describe the sampling distribution from a population that is skewed left with mean 50 and standard deviation 15. Diane obtains 1000 random samples of size n=4 from theâ population, finds the mean of theâ means, and determines the standard deviation of the means. Jack does the sameâ simulation, but obtains 1000 random samples of size n=30 from the population.
(a) Describe the shape you expect for Jack's distribution of sample means. Describe the shape you expect for Diane's distribution of sample means.
(b) What do you expect the mean of Jack's distribution to be? What do you expect the mean of Diane's distribution to be?
(c) What do you expect the standard deviation of Jack's distribution to be? What do you expect the standard deviation of Diane's distribution to be?
Answers
(a) The shape of Jack's distribution of sample means is expected to be bell-shaped, with the mean being centered at the population mean of 50 and the standard deviation being much larger than the standard deviation of the population. This is because Jack is using larger sample sizes, which results in a more accurate estimate of the population mean.
The shape of Diane's distribution of sample means is expected to be similar to Jack's, but less pronounced. This is because Diane is using smaller sample sizes, which results in a less accurate estimate of the population mean.
(b) The mean of Jack's distribution of sample means is expected to be similar to the population mean of 50, but slightly larger due to the larger sample sizes. The mean of Diane's distribution of sample means is also expected to be similar to the population mean of 50, but again slightly larger due to the larger sample sizes.
(c) The standard deviation of Jack's distribution of sample means is expected to be smaller than the standard deviation of the population, because the larger sample sizes result in a more accurate estimate of the population mean. The standard deviation of Diane's distribution of sample means is also expected to be smaller than the standard deviation of the population, but again to a lesser extent due to the smaller sample sizes.
Learn more about probability visit : brainly.in/question/40083838
#SPJ11
. let a ∈ z be an integer of the form a = 4n 3 for some n ∈ z . prove that a has a prime divisor p of the form p = 4m 3 for some m ∈ z .
Answers
The that a must have a Prime divisor of the form p = 4m 3 for some m ∈ z, as required.
To prove that a has a prime divisor p of the form p = 4m 3 for some m ∈ z, we need to use a proof by contradiction. Assume that a does not have a prime divisor of the form p = 4m 3 for any m ∈ z. This means that all prime divisors of a must be of the form p = 4m 1 or p = 2.
First, let's consider the case where all prime divisors of a are of the form p = 4m 1. Since a = 4n 3, we know that it is odd and not divisible by 2. Therefore, all its prime divisors must also be odd, which means they can be expressed as p = 4m 1. However, we can easily see that the product of any number of primes of the form 4m 1 is also of the form 4m 1. This means that a, which is of the form 4n 3, cannot be expressed as a product of primes of the form 4m 1, leading to a contradiction.
Now let's consider the case where all prime divisors of a are of the form p = 2. Since a = 4n 3, it is not divisible by 2^2, so its prime factorization must be a product of 2's. However, we can easily see that no product of powers of 2 can give us a number of the form 4n 3, leading to another contradiction.
Therefore, we can conclude that a must have a prime divisor of the form p = 4m 3 for some m ∈ z, as required.
To know more about divisor .
https://brainly.com/question/30740718
#SPJ11
Since a is odd, it must be of the form a = 4n + 1. Let a = 4n + 1 = p1^a1 · p2^a2 · · · pk^ak be the prime factorization of a. Suppose all prime factors of a are of the form 4m + 1. Then a ≡ 1 (mod 4), which is a contradiction. Therefore, a must have a prime factor of the form 4m + 3.
We prove the contrapositive. Suppose a has no prime divisor of the form p = 4m + 3. We show that a is not of the form a = 4n + 3.
Let a = 4n + 3. Since a is odd, it must have a prime divisor p. Note that p cannot be 2. Also, p cannot be of the form p = 4m + 3, since we assumed a has no such prime divisor. Therefore, p must be of the form p = 4m + 1.
Write a = pk, where k ∈ Z. Then 4n + 3 = pk. Since p is odd, we have 4n ≡ −3 (mod p). Squaring both sides, we get 16n^2 ≡ 9 (mod p).
Now note that 16 ≡ 1 (mod p) and so 16^(p-1) ≡ 1 (mod p) by Fermat's Little Theorem. Therefore, we have
9 = 16n^2 · 16^−2 ≡ n^2 (mod p).
This means that n^2 ≡ 9 (mod p), so p must divide (n−3)(n+3). Since p is of the form 4m + 1, neither n−3 nor n+3 is divisible by p. Therefore, p must divide both n−3 and n+3. This means that p divides their difference, which is 6. Since p is of the form 4m + 1, it cannot divide 2 or 3. Therefore, p must be 5.
But this means that a = pk is divisible by 5, which contradicts the fact that a has no prime divisor of the form 4m + 3. Therefore, we conclude that a cannot be of the form a = 4n + 3.
Know more about prime factorization here:
https://brainly.com/question/29775157
#SPJ11
describe the following solids using inequalities. (a) a cylindrical shell 7 units long, with inside diameter 2 units and outside diameter 3 units
Answers
To describe the cylindrical shell, we can use the following inequalities:
Length: Since the cylindrical shell is 7 units long, we can use the inequality: 0 ≤ z ≤ 7, where z represents the height or the vertical axis.
Inside Diameter: The inside diameter of the cylindrical shell is 2 units. We can use the inequality: (x^2 + y^2) ≥ 1, where x and y represent the coordinates on the horizontal plane and (x^2 + y^2) represents the distance from the origin.
Outside Diameter: The outside diameter of the cylindrical shell is 3 units. We can use the inequality: (x^2 + y^2) ≤ 2.25, where (x^2 + y^2) represents the distance from the origin.
Combining these inequalities, the complete description of the cylindrical shell would be:
0 ≤ z ≤ 7,
(x^2 + y^2) ≥ 1,
(x^2 + y^2) ≤ 2.25.
These inequalities define the region in 3D space that corresponds to the cylindrical shell with a length of 7 units, inside diameter of 2 units, and outside diameter of 3 units.
Learn more about vertical axis here: brainly.com/question/32386232
#SPJ11
please help me with this
Answers
The function y=(x-2)²-1 has vertex (2, -1), focus (2, -3/4) and axis of symmetry is x=2.
1) y=-x²+4x+3
From the given graph,
Direction: Opens Down
Vertex: (2,7)
Focus: (2,27/4)
Axis of Symmetry: x=2
Directrix: y=29/4
To find the x-intercept, substitute in 0 for y and solve for x. To find the y-intercept, substitute in 0 for x and solve for y.
x-intercept(s): (2+√7,0),(2−√7,0)
y-intercept(s): (0,3)
Find the domain by finding where the equation is defined. The range is the set of values that correspond with the domain.
Domain: (−∞,∞),{x|x∈R}
Range: (−∞,7],{y|y≤7}
3) y=(x-2)²-1
Graph the parabola using the direction, vertex, focus, and axis of symmetry.
Direction: Opens Up
Vertex: (2,−1)
Focus: (2,−3/4)
Axis of Symmetry: x=2
Directrix: y=−5/4
To find the x-intercept, substitute in 0 for y and solve for x. To find the y-intercept, substitute in 0 for x and solve for y.
x-intercept(s): (3,0),(1,0)
y-intercept(s): (0,3)
Find the domain by finding where the equation is defined. The range is the set of values that correspond with the domain.
Domain: (−∞,∞),{x|x∈R}
Range: [−1,∞),{y|y≥−1}
Therefore, the function y=(x-2)²-1 has vertex (2, -1), focus (2, -3/4) and axis of symmetry is x=2.
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ1
After observing both the graphs the required fields are described below.
In the given graph of the equation,
y = -x² + 4x + 3
From the graph of the this curve
We can see that,
X - intercept of this graph is at (-0.646 , 0) and (4.646, 0)
Y - intercept of this graph is at (0, 3)
Vertex of this graph is at (2, 7)
Domain is whole real line,
Range is (-∞, 7]
Axis of symmetry is x axis.
Increasing in the interval : (-∞, 2]
Decreasing in the interval : [7, ∞)
In the given graph of the equation,
y = (x-2)² - 1
From the graph of the this curve
We can see that,
X - intercept of this graph is at (1 , 0) and (3, 0)
Y - intercept of this graph is at (0, 3)
Vertex of this graph is at (2, -1)
Domain is real number,
Range is [-1, ∞)
Axis of symmetry is x axis.
Increasing in the interval : (-∞, 1]U[3,∞)
Decreasing in the interval : (1, 3)
To learn more about graph of function visit:
https://brainly.com/question/12934295
#SPJ1
PLEASE HELP!!!
The line plots show the number of kilometers that Jen and Denisha biked each week for 10 weeks.
Based on the data, who is more likely to ride a greater distance in the eleventh week? Move a word to each blank to complete the sentence. ____ is more likely to ride a greater distance because the ____ of her data is greater ^image
Jen
Mean
Mode
Denisha
Range
Answers
Answer: first blank: jen
second blank: mean
Step-by-step explanation:
N/A
solve the initial value problem dy/dx = 1/2 2xy^2/cosy-2x^2y with the initial value, y(1) = pi
Answers
Our final solution is: cosy * y = 1/3 * x^3y^2 - 1/3 * pi^3 - pi
To solve the initial value problem dy/dx = 1/2 2xy^2/cosy-2x^2y with the initial value, y(1) = pi, we need to first separate the variables and integrate both sides.
Starting with the given differential equation, we can rearrange to get:
cosy dy/dx - 2x^2y dy/dx = 1/2 * 2xy^2
Now, we can use the product rule in reverse to rewrite the left-hand side as d/dx (cosy * y) = xy^2.
So, we have:
d/dx (cosy * y) = xy^2
Next, we can integrate both sides with respect to x:
∫d/dx (cosy * y) dx = ∫xy^2 dx
Integrating the left-hand side gives us:
cosy * y = 1/3 * x^3y^2 + C
where C is the constant of integration.
Using the initial value y(1) = pi, we can solve for C:
cos(pi) * pi = 1/3 * 1^3 * pi^2 + C
-1 * pi = 1/3 * pi^3 + C
C = -1/3 * pi^3 - pi
So, our final solution is:
cosy * y = 1/3 * x^3y^2 - 1/3 * pi^3 - pi
Answer in 200 words: In summary, to solve the initial value problem, we first separated the variables and integrated both sides. This allowed us to rewrite the equation in terms of the product rule in reverse and integrate it. We then used the initial value to solve for the constant of integration and obtained the final solution. It is important to remember that when solving initial value problems, we must always use the given initial value to find the constant of integration. Without it, our solution would be incomplete. This type of problem can be challenging, but by following the proper steps and using algebraic manipulation, we can arrive at the correct answer. It is also worth noting that the final solution may not always be in a simplified form, and that is okay. As long as we have solved the initial value problem and obtained a solution that satisfies the given conditions, we have successfully completed the problem.
Learn more on initial value problem here:
https://brainly.com/question/30547172
#SPJ11
1. let x,y, r90 be elements of d4 with y ? r90 and x2 y r90. determine y. show your reasoning.
Answers
The equation x^2 * y = r90 is x^2 * y = d1 * v = r90. The y = v is the unique solution that satisfies the given conditions.
Recall that the dihedral group D4 has eight elements: the identity element e, three rotations r90, r180, r270, and four reflections h, v, d1, d2. We are given that x, y, and r90 are elements of D4, with y not equal to r90, and x^2 * y = r90. We want to determine y.
We can start by examining the possible values of x and x^2. Since x^2 appears in the equation, it's natural to look for elements that, when squared, produce r90. There are two such elements: r270 and d1.
If x = r270, then x^2 = r180 and y = d1, since r180 * d1 = r90. However, this does not satisfy the condition that y is not equal to r90.
If x = d1, then x^2 = r90, and we can write y as x^2 * y * x^(-2), using the fact that x^2 = r90.
y = x^2 * y * x^(-2)
= r90 * y * r270
= r90 * y * r90 * r180
= r90 * y * r90 * d1
Now, since y is not equal to r90, it must be one of the remaining reflections h, v, or d2. But since r90 commutes with all the reflections, we can simply look at the action of y on r90, and see which reflection takes r90 to the image of r90 under y.
r90 * h = v
r90 * v = r270
r90 * d2 = d1
Therefore, y = v. We can check that this satisfies the equation x^2 * y = r90:
x^2 * y = d1 * v = r90
Therefore, y = v is the unique solution that satisfies the given conditions.
Learn more about unique solution here
https://brainly.com/question/12323968
#SPJ11
let a and b be two independent events with p(a) = 0.40 and p(b) = 0.20. which of the following is correct?
Answers
The correct statement regarding the events A and B is that the probability of both events occurring simultaneously, denoted as P(A ∩ B), is equal to zero. This means that A and B are mutually exclusive events, and they cannot occur together.
The explanation for this lies in the fact that they are defined as independent events, which implies that the occurrence or non-occurrence of one event does not affect the probability of the other event happening. In this scenario, we are given that events A and B are independent, with P(A) = 0.40 and P(B) = 0.20. To determine whether they are mutually exclusive, we need to calculate the probability of their intersection, denoted as P(A ∩ B). If P(A ∩ B) is zero, it indicates that A and B cannot occur simultaneously Since A and B are independent events, their probabilities multiply to give the joint probability of both events happening: P(A ∩ B) = P(A) × P(B). In this case, we have P(A ∩ B) = 0.40 × 0.20 = 0.08. As the resulting probability is not zero, it means that the events A and B are not mutually exclusive. Therefore, none of the given statements suggest the correct relationship between A and B. The correct statement is that the probability of both events occurring simultaneously, P(A ∩ B), is equal to zero..
Learn more about joint probability here: brainly.com/question/32099581
#SPJ11
Find the probability that a randomly selected point within the circle falls in the red-shaded square.
4√2
8
8
P = [ ? ]
Answers
Answer:
0.64
Step-by-step explanation:
Area of circle = π r ²
= π (4√2)²
= (4² X √2²) π
= 32π.
area of square = 8 X 8 = 64.
we want P(inside red square)
= 64/(32π)
= 0.64 to nearest one hundredth
A sample of n= 12 scores ranges from a high of X = 7 to a low of X= 4. If these scores are placed in a frequency distribution table, how many X values will be listed in the first column? O a. 12 O b.4 Oc.3 10 d. 7
Answers
The number of X values listed in the first column of the frequency distribution table will be d) 4.
In a frequency distribution table, the first column typically represents the range or interval of the scores. Since the given sample has a range from X = 7 to X = 4, the first column of the frequency distribution table will include the four distinct X values: X = 4, X = 5, X = 6, and X = 7.
hese are the possible values within the given range, and thus, there will be 4 X values listed in the first column. So the correct option is d in this question.
For more questions like Sample click the link below:
https://brainly.com/question/30759604
#SPJ11
compute and sketch the vector assigned to the points =(0,6,1) and =(2,1,0) by the vector field F = (xy, z2, x ). F (P) = F (Q) =
Answers
To compute the vector assigned to the points P=(0,6,1) and Q=(2,1,0) by the vector field F=(xy, z², x), we need to evaluate F(P) and F(Q) as follows:
F(P) = (0)(6), (1²), 0 = (0, 1, 0)
F(Q) = (2)(1), (0²), 2 = (2, 0, 2)
Therefore, the vectors assigned to P and Q are (0, 1, 0) and (2, 0, 2), respectively. To sketch these vectors, we can plot them as arrows starting from the corresponding points on a 3-dimensional coordinate system. The vector assigned to P will point upward along the y-axis, while the vector assigned to Q will point diagonally in the positive x-z direction. The length of each arrow can be arbitrary and does not affect the direction of the vector.
Learn more about diagonally here:
https://brainly.com/question/28592115
#SPJ11
Find the Taylor series generated by f(x) = cos (2x) and centered at πSelect one:a(x−π)−43!(x−π)3+165!(x−π)2−....b)1−41!(x−π)3+42!(x−π)2−...c) 1−42!(x−2π)2+164!(x−2π)4−....d) 1+42!(x−π)2+164!(x−π)4−...e) 1−42!(x−π)2+164!(x−π)4
Answers
For the taylor series generated by f(x) = cos (2x) and centered at π . The correct answer is: e) 1 - 4*(x-π)^2/2 + 16*(x-π)^4/4!
The Taylor series generated by f(x) = cos(2x) and centered at π is:
f(x) ≈ f(π) + f'(π)(x-π) + f''(π)(x-π)^2/2! + f'''(π)(x-π)^3/3! + ...
We need to find the derivatives of f(x) at π:
f(x) = cos(2x)
f'(x) = -2sin(2x)
f''(x) = -4cos(2x)
f'''(x) = 8sin(2x)
Now evaluate the derivatives at x = π:
f(π) = cos(2π) = 1
f'(π) = -2sin(2π) = 0
f''(π) = -4cos(2π) = -4
f'''(π) = 8sin(2π) = 0
Plug the values back into the Taylor series:
f(x) ≈ 1 + 0*(x-π) - 4*(x-π)^2/2! + 0*(x-π)^3/3! + ...
f(x) ≈ 1 - 4*(x-π)^2/2! = 1 - 2*(x-π)^2
Comparing this with the given options, the correct answer is:
e) 1 - 4*(x-π)^2/2 + 16*(x-π)^4/4!
To know more about taylor series refer here:
https://brainly.com/question/29733106?#
#SPJ11
Suppose f(x) has the following properties: - f(x) and all its derivatives exist at x=7, - f(7)=8 - f (x)=f(x)+10 for all x. Enter the first three terms of the Taylor polynomial approximation for f(x) centered at x=7
Answers
The first three terms of the Taylor polynomial approximation for a function f(x) centered at x=a provide an approximation of the function in the vicinity of x=a. These terms are obtained by evaluating the function and its derivatives at the center point a and then multiplying them by the corresponding powers of (x-a).
In this case, the first term is simply the value of the function at x=a, which is f(a). The second term involves the first derivative of f(x) evaluated at x=a, multiplied by (x-a). The third term involves the second derivative of f(x) evaluated at x=a, multiplied by (x-a)^2 divided by 2!. These terms capture the linear and quadratic behavior of the function around the point x=a.
By adding up these terms, we obtain an approximation of the function f(x) near x=a, which becomes more accurate as we include higher-order terms. The Taylor polynomial allows us to estimate the behavior of the function and make predictions in the local neighborhood of the center point a.
To find the first three terms of the Taylor polynomial approximation for f(x) centered at x=7, we can use the properties given.
The first term of the Taylor polynomial is simply the value of the function at x=7, which is f(7) = 8.
The second term is the derivative of f(x) evaluated at x=7, multiplied by (x-7). Since it is stated that all derivatives of f(x) exist at x=7, we can write the second term as f'(7) * (x-7).
The third term is the second derivative of f(x) evaluated at x=7, multiplied by (x-7)^2, divided by 2!. Again, since all derivatives exist at x=7, we can write the third term as f''(7) * (x-7)^2 / 2!.
Putting it all together, the first three terms of the Taylor polynomial approximation for f(x) centered at x=7 are:
8 + f'(7) * (x-7) + f''(7) * (x-7)^2 / 2!
Learn more about function : brainly.com/question/30721594
#SPJ11
If a function f has an inverse and f(x) = -1, then f'(-1)= __ If a function f has an inverse and f(x) = - 1, then f'(-1)=0
Answers
In order for the function to have an inverse, f'(x) ≠ 0. Therefore, we cannot provide a specific value for f'(-1) based on the given information.
A function that reverses the effects of another function is called an inverse function. It links each of the original function's output values to the relevant input value. A function must be one-to-one and onto in order to have an inverse. In other words, the function must be able to handle every potential output value and each input value must translate into a distinct output value.
To find the derivative of the inverse function at a given point, we can use the formula:
(f^(-1))'(y) = 1 / f'(f^(-1)(y))
In this case, we know that f(x) = -1. Let's assume f^(-1)(-1) = x. Then, we have:
f^(-1)'(-1) = 1 / f'(x)
Now, according to the given information, f'(-1) = 0. However, this statement is incorrect because it would lead to division by zero in our formula, which is undefined. In order for the function to have an inverse, f'(x) ≠ 0. Therefore, we cannot provide a specific value for f'(-1) based on the given information.
Learn more about function here:
https://brainly.com/question/2264322
#SPJ11
Let
t= 0
be the point at which the car is just starting to drive
and the bus is even with the car. Find the other time when the vehicles will be the same distance from the intersection
Answers
The other time when the car and the bus will be the same distance from the intersection is Δt units of time after their starting time (t=0), assuming their speeds remain equal throughout the journey.
To find the other time when the car and the bus will be the same distance from the intersection, we need to consider their respective rates of motion. Let's assume the car and the bus are moving in the same direction along a straight road.
Let's denote the distance of the car from the intersection at time t as "d_car(t)" and the distance of the bus from the intersection at time t as "d_bus(t)". We'll also denote their respective rates of motion as "v_car" and "v_bus".
Since the bus is even with the car at time t=0, we can set up the following equation:
d_car(0) = d_bus(0)
Now, let's consider the time when the car and the bus will be the same distance from the intersection. Let's call this time "t_match". At this time, we'll have:
d_car(t_match) = d_bus(t_match)
To find this time, we need to compare their rates of motion. If the car and the bus have different speeds, they will not remain the same distance apart. However, if their speeds are the same, they will remain at the same distance.
Therefore, for the car and the bus to be the same distance from the intersection at a later time, their speeds must be equal (v_car = v_bus).
If their speeds are equal, the other time when the vehicles will be the same distance from the intersection will be t_match = 0 + Δt, where Δt is the time it takes for both vehicles to travel the same distance.
In summary, the other time when the car and the bus will be the same distance from the intersection is Δt units of time after their starting time (t=0), assuming their speeds remain equal throughout the journey.
To know more about speed distance and time, visit:
https://brainly.com/question/31841408
#SPJ11
1. The following sed command is supposed to redact all hyphen-delimited numbers on each line of the input stream; will it operate as expected?
s/[0-9]*-?//g
(a) Yes
(b) No
Answers
Yes, the given sed command will operate as expected to redact all hyphen-delimited numbers on each line of the input stream. Option a is Correct.
The regular expression `[0-9]*-?` matches any sequence of one or more digits followed by a hyphen and an optional hyphen, which is a hyphen followed by zero or more digits. The `//g` flag at the end of the command tells sed to apply the replacement globally, so that all matches on each line are replaced.
For example, if the input stream contains the line "123-456-7890", the sed command will replace the hyphen-delimited number with an empty string, resulting in the line "1234567890". Similarly, if the input stream contains the line "7890-1234-5678", the sed command will also replace the hyphen-delimited number with an empty string, resulting in the line "789012345678". Option a is Correct.
Learn more about hyphen-delimited visit: brainly.com/question/31443704
#SPJ4