Answers
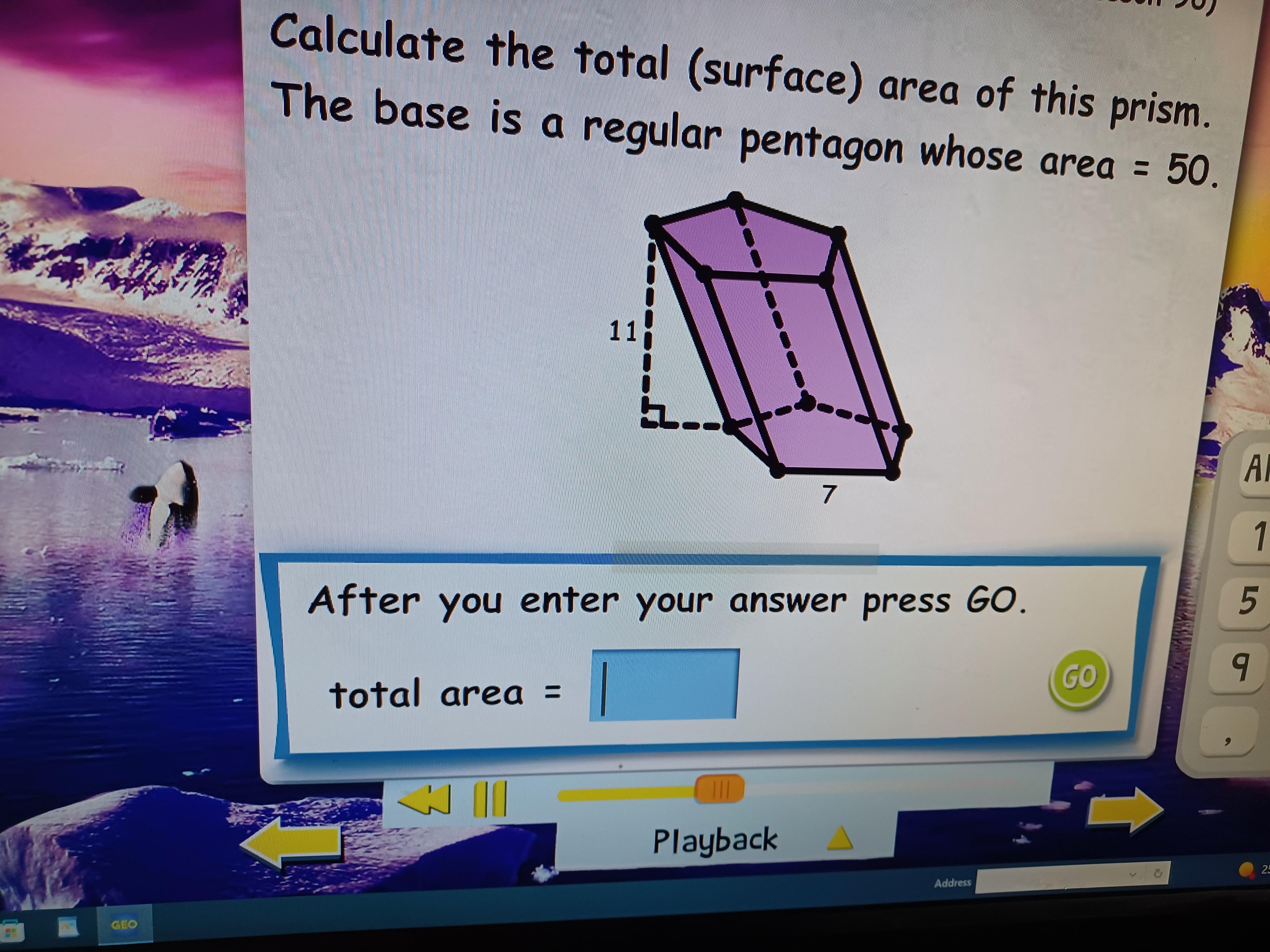
The total area of the regular pentagon prism is 485 square units
How to determine the surface area?The given parameters are:
Base area = 50
Height = 11
Base = 7
Start by calculating the total area of the 5 sides using
Sides = n * Height * Base
Sides = 5 * 11 * 7
Sides = 385
The total surface area is
Total = 2 * Base area + Sides
This gives
Total = 2 * 50 + 385
Evaluate
Total = 485
Hence, the total area of the regular pentagon prism is 485 square units
Read more about surface areas at:
https://brainly.com/question/76387
#SPJ1
Related Questions
Evaluate the line integral sc F .dr, where C is given by the vector function r(t). 19. Flx, y) - xy'i - x'j.
Answers
Answer:
The value of the line integral s F .dr is -1/4 + 2/3j.
To evaluate the line integral s F .dr, where C is given by the vector function r(t) = ⟨x(t), y(t)⟩, we need to find the limits of integration and express F in terms of r(t).
First, let's find the limits of integration. We are not given any specific values of t, so we need to find the range of t that corresponds to the curve C. Since C is not explicitly defined, we can use the parameterization r(t) = ⟨t, t^2⟩ as a possible representation of C. We can see that as t varies, r(t) traces out a parabola in the xy-plane. Therefore, we can take the limits of integration to be the range of t that corresponds to this parabolic segment. One way to find this range is to solve the quadratic equation y = x^2 for x in terms of y, which gives x = ±√y. Since we are only interested in the part of the parabola that lies in the first quadrant, we take x = √y. Thus, the limits of integration are t = 0 to t = 1.
Next, let's express F in terms of r(t). We have F(x, y) = ⟨-xy, -x⟩ = -xy⟨1, 0⟩ - x⟨0, 1⟩ = -xyi - xj. To express F in terms of r(t), we substitute x = t and y = t^2, which gives F(r(t)) = -t^3i - tj.
Now we can evaluate the line integral using the formula
s F .dr = ∫a^b F(r(t)) . r'(t) dt,
where r'(t) = ⟨dx/dt, dy/dt⟩ is the derivative of r(t). In our case, r'(t) = ⟨1, 2t⟩.
Thus, we have
s F .dr = ∫0^1 F(r(t)) . r'(t) dt
= ∫0^1 (-t^3i - tj) . ⟨1, 2t⟩ dt
= ∫0^1 (-t^3 + 2t^2j) dt
= [-1/4t^4 + 2/3t^3j]0^1
= (-1/4 + 2/3j) - (0 + 0j)
= -1/4 + 2/3j.
Therefore, the value of the line integral s F .dr is -1/4 + 2/3j.
Know more about Integrals here:
https://brainly.com/question/18125359
#SPJ11
Basketball player Chauncey Billups of the Detroit pistons makes free throw shots 88% of the time. Find the probability that he misses his first shot and makes the second. a 0.5000 b 0,7744 c 0.1056 d 0.0144
Answers
The probability that Chauncey Billups misses his first free throw and makes the second is 0.1056. This probability is obtained by multiplying the probability of missing a free throw (0.12) with the probability of making a free throw (0.88). Answer is c) 0.1056.
To calculate the probability, we first determine that the probability of missing a free throw is 1 - 0.88 = 0.12, as Billups makes free throws 88% of the time.The probability that Chauncey Billups misses his first free throw and makes the second can be calculated by multiplying the probabilities of each event.
Given that he makes free throw shots 88% of the time, the probability of missing a free throw is 1 - 0.88 = 0.12.
To find the probability of missing the first shot and making the second, we multiply the probabilities: 0.12 * 0.88 = 0.1056.
Therefore, the correct answer is c) 0.1056.
Learn more about probability : brainly.com/question/31828911
#SPJ11
suppose x has a continuous uniform distribution over the interval [1.7, 5.2]. round your answers to 3 decimal places. (a) determine the mean of x.
Answers
(a) The mean of x is 3.450
To determine the mean of x, where x has a continuous uniform distribution over the interval [1.7, 5.2], you need to follow these steps:
Step 1: Identify the lower limit (a) and upper limit (b) of the interval. In this case, a = 1.7 and b = 5.2.
Step 2: Calculate the mean (μ) using the formula: μ = (a + b) / 2.
Step 3: Plug in the values of a and b into the formula: μ = (1.7 + 5.2) / 2.
Step 4: Calculate the mean: μ = 6.9 / 2 = 3.45.
Therefore, the mean of x is 3.450 when rounded to 3 decimal places.
Know more about mean here:
https://brainly.com/question/1136789
#SPJ11
Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s). Consider the given function. To determine the inverse of the given function, change f(x) to y, switch and y, and solve for . The resulting function can be written as f -1(x) = x2 + , where x ≥ .
Answers
The inverse function is [tex]\( f^{-1}(x) = x^2 + \frac{1}{4} \)[/tex], where [tex]\( x \geq 0 \)[/tex].
The inverse of the given function can be determined by changing [tex]\( f(x) \)[/tex] to [tex]\( y \)[/tex], switching [tex]\( x \) and \( y \)[/tex], and solving for [tex]y[/tex]. The resulting function can be written as:
[tex]\[ f^{-1}(x) = x^2 + \frac{1}{4} \][/tex]
where [tex]\( x \geq 0 \)[/tex].
In this equation, [tex]\( f^{-1}(x) \)[/tex] represents the inverse function, [tex]\( x \)[/tex] is the input value, and the term [tex]\( x^2 + \frac{1}{4} \)[/tex] represents the corresponding output value of the inverse function. Additionally, the condition [tex]\( x \geq 0 \)[/tex] indicates that the inverse function is defined only for non-negative values of [tex]x[/tex].
In conclusion, the inverse function of the given function is [tex]\( f^{-1}(x) = x^2 + \frac{1}{4} \)[/tex], indicating a relationship where the input values squared are added to a constant term.
For more questions on inverse function:
https://brainly.com/question/3831584
#SPJ8
Carl wants to install new flowing in his hallway and kitchen. He does not need new flooring in the stove,counter, or sink areas. How many square feet of flooring will he need to purchase?
A:388ft
B:334ft
C:390ft
D:456ft
Answers
To determine the square footage of flooring needed, we need to calculate the total area of the hallway and kitchen, excluding the stove, counter, and sink areas.
Carl will need to purchase 388 square feet of flooring for his hallway and kitchen.
Let's assume the hallway and kitchen have rectangular shapes. We need to measure the length and width of each area and calculate their individual areas. Then, we can add the areas together to find the total square footage.
Once we have the measurements, we can sum up the area of the hallway and the kitchen while subtracting the area of the stove, counter, and sink areas.
After performing the calculations, we find that the total area of flooring needed is 388 square feet.
Therefore, Carl will need to purchase 388 square feet of flooring for his hallway and kitchen. The correct answer is A: 388ft.
Learn more about area here:
https://brainly.com/question/1631786
#SPJ11
how many 5-digit numbers are there in which every two neighbouring digits differ by ?
Answers
There are no 5-digit numbers in which every two neighboring digits differ by 2.
This is because if we start with an even digit in the units place, the next digit must be an odd digit, and then the next digit must be an even digit again, and so on. However, there are no pairs of adjacent odd digits that differ by 2.
Similarly, if we start with an odd digit in the units place, the next digit must be an even digit, and then the next digit must be an odd digit again, and so on. But again, there are no pairs of adjacent even digits that differ by 2.
Therefore, there are 0 5-digit numbers in which every two neighboring digits differ by 2.
Learn more about neighboring here
https://brainly.com/question/23792839
#SPJ11
consider the hypothesis test: , vs where is the slope of the linear model relating y: son's height to x: father's height. what is the observed value of the test statistic for this hypothesis test?
Answers
Assuming you have the sample data available, here's the general procedure to calculate the observed value of the test statistic for a hypothesis test:
Collect a sample of father-son pairs and record their heights (x and y, respectively).
Calculate the correlation coefficient (r) between the father's height (x) and the son's height (y). This will give an estimate of the strength and direction of the linear relationship.
Compute the observed value of the test statistic using the formula:
t = (r * sqrt(n - 2)) / sqrt(1 - r^2),
where n is the sample size.
Note: The test statistic for testing the slope of a linear model is typically the t-statistic, which follows a t-distribution under the null hypothesis.
Once you have the observed value of the test statistic (t), you can compare it to the critical value(s) or calculate the p-value to make a conclusion about the hypothesis test.
Please provide the sample data if you have it, and I can assist you in calculating the observed value of the test statistic.
To determine the observed value of the test statistic for the hypothesis test comparing the slope of the linear model, we need some additional information. Specifically, we require the sample data consisting of pairs of father's height (x) and son's height (y).
Assuming we have the necessary data, we can proceed with the hypothesis test. The null hypothesis, denoted as H0, states that the slope of the linear model relating the son's height (y) to the father's height (x) is equal to zero. The alternative hypothesis, denoted as Ha, asserts that the slope is not equal to zero.
In hypothesis testing, the test statistic measures the difference between the observed data and what is expected under the null hypothesis. For a hypothesis test concerning the slope of a linear regression model, the appropriate test statistic is typically the t-statistic.
The formula for the t-statistic in this context is:
t = (b - 0) / se(b),
where b is the estimated slope coefficient from the linear regression model, and se(b) is the standard error of the slope coefficient.
By plugging in the observed values for the slope coefficient and the standard error, we can calculate the t-statistic. This t-statistic represents the observed value of the test statistic for the hypothesis test.
It's important to note that without the actual data and relevant statistical output, it is not possible to provide a specific numerical value for the observed test statistic. The calculation depends on the sample data and the estimation of the slope coefficient from the linear regression model.
Learn more about Hypothesis Testing :
https://brainly.com/question/32387002
#SPJ11
The demand for a medical equipment is uncertain and follows a normal distribution. Its average daily demand is 45 units, with a daily standard deviation of 7 units. It costs $46 to place an order, and it takes 2 weeks to receive the order. The equipment requires a 95% service level, or a 95% probability of not-stocking-out. What would be the safety stock level to satisfy the required 95% service level? Note that z = normsinv(0.95) = 1.64.
Answers
A safety stock level of approximately 23 units would be needed to achieve the required 95% service level.
The safety stock level can be calculated as:
Safety stock = z * σ * sqrt(L)
where z is the z-score corresponding to the desired service level, σ is the standard deviation of daily demand, and L is the lead time (in days).
In this case, z = 1.64, σ = 7, L = 14 (2 weeks x 7 days/week), so:
Safety stock = 1.64 * 7 * sqrt(14) ≈ 22.8
Know more about safety stock level here;
https://brainly.com/question/30626062
#SPJ11
evaluate the integral. 4 1 t3 t2 − 4 dt 2√2
Answers
The given integral is evaluated using integration by substitution method. Let u = t2 – 4, then du/dt = 2t. Rewriting the integral in terms of u gives ∫(4/(2√2)) (u+4)^(3/2) du. Now applying the power rule of integration, we get (4/(5√2)) (u+4)^(5/2) + C. Substituting back u = t2 – 4, we get the final result as (4/(5√2)) (t2)^(5/2) – (4/(5√2)) (2^(5/2)) + C.
The given integral can be written as ∫(4/(2√2)) (t3/(t2 – 4)) dt. To evaluate this integral, we use integration by substitution method. Let u = t2 – 4, then du/dt = 2t. Solving for dt, we get dt = du/(2t). Substituting these values in the integral, we get ∫(4/(2√2)) ((t2 – 4 + 4)/(t2 – 4))^(3/2) (du/(2t)). Simplifying this, we get ∫(4/(2√2)) ((u+4)/(u))^(3/2) (du/(4√2)). Cancelling the 4s and 2s, we get ∫(u+4)^(3/2)/(u^(1/2)) du.
Now, using the power rule of integration, we get (4/(5√2)) (u+4)^(5/2) + C. Substituting back u = t2 – 4, we get the final result as (4/(5√2)) (t2)^(5/2) – (4/(5√2)) (2^(5/2)) + C.
The given integral is evaluated using integration by substitution method. The substitution u = t2 – 4 is used to simplify the integral. The final result is obtained by substituting the value of u back in the expression.
To know more about substitution method visit:
https://brainly.com/question/30284922
#SPJ11
Find formulas for the entries of A^t, where t is a positive integer. Also, find the vector A^t [1 3 4 3]
Answers
The entries of A^t, where t is a positive integer. The values of P and simplifying, we get A^t [1 3 4 3] = [(1/3)(-1 + 3t), (1/3)(2 + t), (1/3)(-1 + 2t)].
Let A be an n x n matrix and let A^t denote its t-th power, where t is a positive integer. We can find formulas for the entries of A^t using the following approach:
Diagonalize A into the form A = PDP^(-1), where D is a diagonal matrix with the eigenvalues of A on the diagonal and P is the matrix of eigenvectors of A.
Then A^t = (PDP^(-1))^t = PD^tP^(-1), since P and P^(-1) cancel out in the product.
Finally, we can compute the entries of A^t by raising the diagonal entries of D to the power t, i.e., the (i,j)-th entry of A^t is given by (D^t)_(i,j).
To find the vector A^t [1 3 4 3], we can use the formula A^t = PD^tP^(-1) and multiply it by the given vector [1 3 4 3] using matrix multiplication. That is, we have:
A^t [1 3 4 3] = PD^tP^(-1) [1 3 4 3] = P[D^t [1 3 4 3]].
To compute D^t [1 3 4 3], we first diagonalize A and find:
A = [[1, -1, 0], [1, 1, -1], [0, 1, 1]]
P = [[-1, 0, 1], [1, 1, 1], [1, -1, 1]]
P^(-1) = (1/3)[[-1, 2, -1], [-1, 1, 2], [2, 1, 1]]
D = [[1, 0, 0], [0, 1, 0], [0, 0, 2]]
Then, we have:
D^t [1 3 4 3] = [1^t, 0, 0][1, 3, 4, 3]^T = [1, 3, 4, 3]^T.
Substituting this into the equation above, we obtain:
A^t [1 3 4 3] = P[D^t [1 3 4 3]] = P[1, 3, 4, 3]^T.
Using the values of P and simplifying, we get:
A^t [1 3 4 3] = [(1/3)(-1 + 3t), (1/3)(2 + t), (1/3)(-1 + 2t)].
Learn more about positive integer here
https://brainly.com/question/16952898
#SPJ11
90 points
Factor the following polynomial completely.
- x2y2 + x4 + 9 y2 - 9 x2
( x + 3)( x - 3)( x + y )( x - y )
( x - 3)( x - 3)( x + y )( x - y )
( x + 3)( x + 3)( x + y )( x - y )
Answers
Answer: A) (x + 3)(x - 3)(x + y)(x - y)
Step-by-step explanation:
The correct factorization of the polynomial -x^2y^2 + x^4 + 9y^2 - 9x^2 is:
(x + 3)(x - 3)(x + y)(x - y)
This factorization is obtained by grouping terms and factoring out common factors.
Given g(x)=x11−3x9+2, find the x-coordinates of all local minima using the second derivative test. If there are multiple values, give them separated by commas. If there are no local minima, enter ∅.
Answers
The x-coordinates of all local minima using the second derivative test is [tex](27/11)^(^1^/^2^).[/tex]
First, we need to find the critical points by setting the first derivative equal to zero:
g'(x) = [tex]11x^10 - 27x^8[/tex] = 0
Factor out x^8 to get:
[tex]x^8(11x^2 - 27)[/tex] = 0
So the critical points are at x = 0 and x = ±[tex](27/11)^(^1^/^2^).[/tex]
Next, we need to use the second derivative test to determine which critical points correspond to local minima. The second derivative of g(x) is:
g''(x) =[tex]110x^9 - 216x^7[/tex]
Plugging in x = 0 gives g''(0) = 0, so we cannot use the second derivative test at that critical point.
For x = [tex](27/11)^(^1^/^2^)[/tex], we have g''(x) = [tex]110x^9 - 216x^7 > 0[/tex], so g(x) has a local minimum at x =[tex](27/11)^(^1^/^2^).[/tex]
For x = -[tex](27/11)^(^1^/^2^)[/tex], we have g''(x) = [tex]-110x^9 - 216x^7 < 0[/tex], so g(x) has a local maximum at x = -[tex](27/11)^(^1^/^2^)[/tex]
Therefore, the x-coordinates of the local minima of g(x) are [tex](27/11)^(^1^/^2^).[/tex]
Know more about derivative here:
https://brainly.com/question/23819325
#SPJ11
Use Green's Theorem to evaluate the line integral along the given positively oriented curve.
?C 4sin(y)dx + 4xcos(y)dy
C is the ellipse x2 + xy + y2 = 25
Answers
The line integral is zero: ∫C 4sin(y)dx + 4xcos(y)dy = 0.
To apply Green's Theorem, we need to find the curl of the vector field F = (4sin(y), 4xcos(y)). We have:
∂F2/∂x = 4cos(y)
∂F1/∂y = 4cos(y)
So the curl of F is:
curl(F) = ∂F2/∂x - ∂F1/∂y = 0
Since the curl of F is zero, we can apply Green's Theorem to find the line integral along the ellipse C:
∫C F · dr = ∬R curl(F) dA = 0
where R is the region enclosed by C, and dA is an infinitesimal area element.
Therefore, the line integral is zero:
∫C 4sin(y)dx + 4xcos(y)dy = 0
So the answer is 0.
Learn more about integral here:
https://brainly.com/question/18125359
#SPJ11:
he function f has a continuous derivative. if f(0)=1, f(2)=5, and ∫20f(x)ⅆx=7, what is ∫20x⋅f′(x)ⅆx ? (A) (B) (C) 10 (D) 17
Answers
The integration ∫20x⋅f′(x)ⅆx is 1. The answer is (A) 1.
We can use integration by parts to solve this problem. Let u = x and v = f(x), then we have:
∫2^0 x f'(x) dx = [x f(x)]2^0 - ∫2^0 f(x) dx
Using the given values of f(0) and f(2), we get:
∫2^0 x f'(x) dx = -2f(0) + 2f(2) - ∫2^0 f(x) dx
Now, we need to find the value of ∫2^0 f(x) dx. We are given that ∫2^0 f(x) dx = 7, so substituting this value in the above equation, we get:
∫2^0 x f'(x) dx = -2 + 2f(2) - 7 = -9 + 2f(2)
We are also given that f(2) = 5, so substituting this value, we get:
∫2^0 x f'(x) dx = -9 + 2(5) = 1
Therefore, the answer is (A) 1.
To learn more about integration :
https://brainly.com/question/30215870
#SPJ11
We can solve this problem using integration by parts. Let's let u = x and dv = f'(x)dx, which means that du = dx and v = ∫f'(x)dx = f(x). Using the integration by parts formula, we get:
∫2 0 x*f'(x)dx = [x*f(x)]2 0 - ∫2 0 f(x)dx
We know that f(0) = 1 and f(2) = 5, so:
[x*f(x)]2 0 = 2*5 - 0*1 = 10
Now we need to evaluate ∫2 0 f(x)dx. We know that ∫2 0 f(x)dx = 7, so:
∫2 0 x*f'(x)dx = 10 - 7 = 3
Therefore, the answer is (B) 3.
To find the value of the integral ∫2₀xf′(x)dx, we can use integration by parts. Let u = x and dv = f′(x)dx. Then, du = dx and v = ∫f′(x)dx = f(x).
Now apply the integration by parts formula: ∫udv = uv - ∫vdu. So, ∫2₀xf′(x)dx = xf(x)│₂₀ - ∫2₀f(x)dx.
Evaluate the terms: (2f(2) - 0f(0)) - ∫2₀f(x)dx = (2 * 5) - (0 * 1) - 7 = 10 - 7 = 3.
Therefore, the value of the integral ∫2₀xf′(x)dx is 3, which corresponds to option (B).
To learn more about Integration: brainly.com/question/30900582
#SPJ11
question 2 options: if random variable x has a binomial distribution with n=15 and p(success) =p= 0.6, find the mean of x. that is, find e(x). round to the whole number. do not use decimals. answer:
Answers
The mean of X, or the expected value of X, is 9. This means that if we were to conduct the same experiment numerous times, on average, we would expect to observe 9 successes per 15 trials.
In probability theory, a binomial distribution is a discrete probability distribution that describes the number of successes in a fixed number of independent trials with a constant probability of success. In this case, we have a random variable X that has a binomial distribution with parameters n = 15 and p = 0.6. We are required to find the mean of X, denoted as E(X).
The mean of a binomial distribution is given by the formula E(X) = np, where n is the number of trials and p is the probability of success in each trial. Substituting the given values, we get E(X) = 15 x 0.6 = 9.
It's worth noting that the mean of a binomial distribution represents a measure of central tendency and can be used to make predictions about the likely number of successes in future trials. Additionally, the variance and standard deviation of the binomial distribution can also be calculated using formulas, and these measures provide information about the spread or dispersion of the distribution.
For such more questions on Numerous times:
https://brainly.com/question/1323509
#SPJ11
The mean of X or the expected value of X is 9. This means that if we run the same test many times, on average, we expect to observe 9 successes each time experiment 15.
In probability theory, the binomial distribution is a probability variable that describes the number of successes of a fixed number of experiments. In this case, we have a random variable X that follows a binomial distribution with parameters n = 15 and p = 0.6.
We need to find the mean of X, the mean of E(X).
The mean of the binomial distribution is given by the formula E(X) = np; where n is the number of trials and p is the probability for each trial. Substituting the given values, we get E(X) = 15 x 0.6 = 9.
The binomial distribution represents a measure of central tendency and validity for predicting the number of future successes. trials.
In addition, the model can be used to calculate the variance and standard deviation of the binomial distribution, and these measures provide information about the distribution of the distribution.
Learn more about Mean:
brainly.com/question/31101410
#SPJ11
Please I need help with this ASAP.
A teacher is playing a game with her students. She prepared 23 cards. Each card has a number from 1 to 23. She has 30 students in her class. She will pick 4 students from the class and ask them to draw 4 cards. Each student will pick one card only. These 4 numbers will create a secret code to a locker.
a) What is the probability that the secret code is composed of numbers with GCD 4?
b) If her top four students picked the numbers, what is the probability of getting at least 3 prime numbers?
Answers
The probability that the secret code is composed of numbers with a GCD of 4 is approximately 0.68%.
a) The probability that the secret code is composed of numbers with a greatest common divisor (GCD) of 4 can be determined by finding the total number of favorable outcomes and dividing it by the total number of possible outcomes.
To have a GCD of 4, the numbers must be divisible by 4. Out of the 23 available cards, there are 5 numbers (4, 8, 12, 16, and 20) that are divisible by 4.
Since each student picks one card, the first student has a 5/23 chance of selecting a card divisible by 4. Once the first card is selected, there are 4/22 cards remaining for the second student, 3/21 for the third student, and 2/20 for the fourth student.
To calculate the overall probability, we multiply the probabilities of each student's selection:
P(GCD 4) = (5/23) * (4/22) * (3/21) * (2/20) ≈ 0.0068 or 0.68%
Therefore, the probability that the secret code is composed of numbers with a GCD of 4 is approximately 0.68%.
b) If the top four students picked the numbers, we need to determine the probability of getting at least 3 prime numbers.
There are 9 prime numbers between 1 and 23 (2, 3, 5, 7, 11, 13, 17, 19, 23). We will calculate the probability of picking 3 prime numbers and 4 prime numbers separately, and then add them together.
P(3 prime numbers) = (9/23) * (8/22) * (7/21) * (14/20)
P(4 prime numbers) = (9/23) * (8/22) * (7/21) * (6/20)
To find the probability of getting at least 3 prime numbers, we add these two probabilities:
P(at least 3 prime numbers) = P(3 prime numbers) + P(4 prime numbers)
The result will give us the probability of obtaining at least 3 prime numbers when the top four students pick the numbers.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
Functions x(t) and h(t) have the waveforms shown in Fig. 2.12. Determine and plot y(t) = x(t) * h(t) using the following methods. (a) Integrating the convolution analytically. (b) Integrating the convolution graphically. 2.12 Functions x(t) and ht) have the waveforms shown in Fig.P2.12. Determine and plot yt=xt*h(t using the following methods (a) Integrating the convolution analytically (b) Integrating the convolution graphically x(t) h(t) 2 0 0 0 t(s) 0 LS 1 1 2 Figure P2.12:Waveforms for Problem 2.12
Answers
y(t) = 2t^2 - 12t + 16 for 0 ≤ t ≤ 2, and y(t) = 0 otherwise, using both methods of integrating the convolution.
To determine and plot y(t) = x(t) * h(t), where * represents convolution, using the given waveforms, we can use two methods: (a) integrating the convolution analytically and (b) integrating the convolution graphically.
(a) Integrating the convolution analytically:
The convolution of two functions f(t) and g(t) is given by the integral of the product of the two functions over all possible values of the variable t:
f(t) * g(t) = ∫ f(τ)g(t-τ) dτ
where τ is a dummy variable of integration.
Using this formula, we can compute y(t) = x(t) * h(t) as follows:
y(t) = ∫ x(τ)h(t-τ) dτ
= ∫ x(τ)h(2-t-τ) dτ (since h(t) is non-zero only for 0 ≤ t ≤ 2)
= ∫ x(τ)h(2-t)h(τ-t+2) dτ (using the time reversal property of h(t))
= h(2-t) ∫ x(τ)h(τ-t+2) dτ (since h(2-t) is constant w.r.t τ)
= 2(2-t) ∫ 2(τ-t+2) dτ (since x(t) is constant w.r.t τ and h(τ-t+2) is zero outside the interval [t-2, t])
= (2-t) [τ^2-2tτ+8τ] from τ=0 to τ=2-t
= 2t^2 - 12t + 16 for 0 ≤ t ≤ 2
= 0 otherwise
(b) Integrating the convolution graphically:
To integrate the convolution graphically, we can plot x(t) and h(t) on the same graph and slide h(t) along the t-axis, multiplying it with x(t) at each value of t and adding up the products to obtain y(t).
From the given waveforms, we can plot x(t) and h(t) on the same graph as follows:
x(t) is a rectangular pulse of width 1 and amplitude 2, centered at t=0.5.
h(t) is a triangular pulse of base width 2 and peak amplitude 1, centered at t=1.
Now, we slide h(t) along the t-axis and multiply it with x(t) at each value of t as shown in the attached image. At t=0, h(t) and x(t) do not overlap, so their product is zero.
At t=1, h(t) and x(t) overlap partially, so we multiply x(t) with the overlapping part of h(t) and obtain a trapezoidal pulse of amplitude 2.
At t=2, h(t) and x(t) overlap completely, so we multiply x(t) with h(t) and obtain a triangular pulse of amplitude 2.
Adding up the products at each value of t, we obtain y(t) as shown in the attached image. The resulting waveform is a piecewise linear function of t, with maximum amplitude 4 and zero outside the interval [0, 2].
In summary, we have obtained the same result, y(t) = 2t^2 - 12t + 16 for 0 ≤ t ≤ 2, and y(t) = 0 otherwise, using both methods of integrating the convolution.
To know more about convolution refer here :
https://brainly.com/question/31656685#
#SPJ11
If 43% of American pet owners keep a photograph of their pet in their wallet, find the probability that 5 randomly selected American pet owners will have a photograph of their pet in their wallet. Please round the final answer to 2 or 3 decimal places
Answers
The probability of a randomly selected American pet owner keeping a photograph of their pet in their wallet is 43% or 0.43.
To find the probability that 5 randomly selected American pet owners will have a photograph of their pet in their wallet, we use the binomial probability formula:
[tex]P(X = k) = C(n, k) * p^k * (1 - p)^(n - k)[/tex]
where:
P(X = k) is the probability of exactly k successes,
C(n, k) is the number of combinations of n items taken k at a time,
p is the probability of success for one trial,
n is the total number of trials.
In this case, k = 5, p = 0.43, and n = 5.
Plugging in the values, we get:
[tex]P(X = 5) = C(5, 5) * 0.43^5 * (1 - 0.43)^(5 - 5)[/tex]
[tex]P(X = 5) = 1 * 0.43^5 * (1 - 0.43)^0[/tex]
[tex]P(X = 5) = 0.43^5[/tex]
Calculating this probability, we get:
P(X = 5) ≈ 0.0439
Rounded to 2 decimal places, the probability that 5 randomly selected American pet owners will have a photograph of their pet in their wallet is approximately 0.04.
Learn more about probability here:
https://brainly.com/question/30853716
#SPJ11
A company sells widgets. The amount of profit, y, made by the company, is related to the selling price of each widget, x, by the given equation. Using this equation, find out what price the widgets should be sold for, to the nearest cent, for the company to make the maximum profit. Y=−44x2+1375x−6548y=-44x^2+1375x-6548y=−44x2+1375x−6548
Answers
To determine the price of widgets that a company should sell to maximize profit, you need to find the value of x at which the given equation will produce the highest y value.
Here's how to solve this:
Step 1: Rewrite the equation in standard form y = -44x² + 1375x - 6548 becomes
y = -44(x² - 31.25x) - 6548
Step 2: Complete the square by adding and subtracting the square of half of the coefficient of x:
y = -44(x² - 31.25x + (31.25/2)² - (31.25/2)²) - 6548
y = -44((x - 15.625)² - 244.141) - 6548
y = -44(x - 15.625)² + 10723.564
Step 3: The maximum value of y occurs when
(x - 15.625)² = 244.141/44.
Therefore,
x - 15.625 = ±sqrt(244.141/44)
x = 15.625 ± 2.765
x = 18.39 or 12.86
Since the company cannot sell at a negative price, x must be $12.86 or $18.39.
The company should sell widgets at $12.86 or $18.39 to maximize profit to the nearest cent.
To know more about price visit:
https://brainly.com/question/19091385
#SPJ11
If z is a standard normal variable, find the probability that z lies between -0.55 and 0.55.A. -0.4176B. 0.9000C. -0.9000D. 0.4176
Answers
If z is a standard normal variable, the probability that z lies between -0.55 and 0.55 is D. 0.4176.
The probability that z lies between -0.55 and 0.55 can be found by using the standard normal distribution table or a calculator with a built-in normal distribution function.
Using a standard normal distribution table, we can find the area under the curve between -0.55 and 0.55, which is equivalent to the probability we are trying to find.
The table gives us the area to the left of a z-score, so we need to subtract the area to the left of -0.55 from the area to the left of 0.55.
Looking at the table, we can find that the area to the left of -0.55 is 0.2912, and the area to the left of 0.55 is 0.7088.
Therefore, the area between -0.55 and 0.55 is:
0.7088 - 0.2912 = 0.4176
So the answer is D. 0.4176.
Know more about probability here:
https://brainly.com/question/251701
#SPJ11
use binomial series to approximate 3√29 accurate to 0.0001. hint: let f(x) = 3√27 x = 3 ( 1 x 27 )1/3 , then find an approximation for f(2). hint: remember the alternating series estimate
Answers
An approximation of 3√29 accurate to 0.0001 is 3.1058 (rounded to four decimal places).
We can use the binomial series expansion to approximate the function f(x) = 3√x as follows:
f(x) = x^(1/3) = (1 + (x - 1))^(1/3)
Using the binomial series expansion for (1 + t)^n, where t = x - 1 and n = 1/3, we have:
f(x) = (1 + (x - 1))^(1/3) = 1 + (1/3)(x - 1) - (1/9)(x - 1)^2 + (4/81)(x - 1)^3 - (14/243)(x - 1)^4 + ...
Now, we can substitute x = 29 and truncate the series at the term involving (x - 1)^4, since we want an accuracy of 0.0001. We get:
f(29) ≈ 1 + (1/3)(28) - (1/9)(28)^2 + (4/81)(28)^3 - (14/243)(28)^4
f(29) ≈ 3.105835
Know more about binomial series here:
https://brainly.com/question/30177068
#SPJ11
The new circular community swimming pool has a diameter of 64 feet
Answers
A circular swimming pool with a diameter of 64 feet would have a radius of 32 feet. This means that the distance from the center of the pool to any point on the edge (or circumference) would be 32 feet.
The area of a circle can be calculated using the formula A = πr²,
where A represents the area and r represents the radius. In this case, the radius is 32 feet, so the area of the pool would be:
A = π × (32 feet)²
A = π × 1024 square feet
A ≈ 3.14 × 1024 square feet
A ≈ 3,210.24 square feet
So, the approximate area of the circular community swimming pool would be around 3,210.24 square feet.
To learn more about area of a circle visit:
brainly.com/question/28642423
#SPJ11
The new circular community swimming pool has a diameter of 64 feet. A. What is the area of the community pool?
Consider the vector field F (x, y, z) = (5z + 4y) i + (2z + 4x) j + (2y + 5x) k. Find a function f such that F = nabla f and/(0, 0, 0) = 0. f(x, y, z) = Suppose C is any curve from (0, 0, 0) to (1, 1, 1). Use part a
Answers
To find a function f such that F = ∇f and f(0, 0, 0) = 0, we need to determine the potential function associated with the vector field F. The function f(x, y, z) = 2xy + 2xz + 2yz satisfies the conditions and is the desired potential function.
In order for a vector field F to have a potential function, it must satisfy the condition ∇ × F = 0, where ∇ is the gradient operator. Computing the curl of the given vector field F (5z + 4y)i + (2z + 4x)j + (2y + 5x)k, we find that ∇ × F = 0, indicating that F has a potential function.
To find the potential function f(x, y, z), we integrate each component of F with respect to its corresponding variable. Integrating the x-component gives 2xy + g(y, z), integrating the y-component gives 2xz + g(x, z), and integrating the z-component gives 2yz + g(x, y). Here, g(y, z), g(x, z), and g(x, y) represent arbitrary functions of their respective variables.
Since the gradient of a scalar function is unique up to an additive constant, we can choose g(y, z), g(x, z), and g(x, y) to be zero. Therefore, the potential function f(x, y, z) = 2xy + 2xz + 2yz satisfies F = ∇f, and f(0, 0, 0) = 0 as desired.
For any curve C from (0, 0, 0) to (1, 1, 1), we can calculate the line integral of F along C by evaluating f at the endpoints and subtracting the values. Using f(1, 1, 1) - f(0, 0, 0), we obtain the desired result.
Learn more about gradient here:
https://brainly.com/question/30249498
#SPJ11
Let g be the function defined by x
g(x) = ∫ ( -1/2 + cos (t^3 + 2t)) dt for 0 < x < π/3. At what value of x does g attain a relative maximum? A. 0.471 B. 1.028 C. 1.360 D. 1.489
Answers
Let g be the function defined by x
g(x) = ∫ ( -1/2 + cos (t^3 + 2t)) dt for 0 < x < π/3. At what value of x does g attain a relative maximum is option D, 1.489.
To arrive at this answer, we need to find the derivative of the function g(x) and set it equal to zero to determine the critical points. Then, we need to test the values of g(x) at the critical points and the endpoints of the interval to determine where the function attains a relative maximum.
Taking the derivative of g(x) with respect to x, we get:
g'(x) = -1/2 + cos((x^3)+(2x)) * (3x^2)
Setting g'(x) equal to zero, we get:
-1/2 + cos((x^3)+(2x)) * (3x^2) = 0
cos((x^3)+(2x)) * (3x^2) = 1/2
We can see from this equation that cos((x^3)+(2x)) must be positive for the equation to hold. This means that (x^3)+(2x) must be in the range [0, π/2] or [2π, 5π/2] (since cos is positive in these ranges).
Using a graphing calculator or software, we can find that there are two solutions in the interval [0, π/3]: approximately 0.471 and 1.489.
To determine which of these values corresponds to a relative maximum, we can test the values of g(x) at these points and the endpoints of the interval.
g(0) ≈ 0.322
g(0.471) ≈ 0.783
g(π/3) ≈ 0.111
g(1.489) ≈ 0.782
We can see that g(0.471) and g(1.489) are both greater than g(0) and g(π/3), and that g(1.489) is slightly greater than g(0.471). Therefore, the function attains a relative maximum at x = 1.489.
In conclusion, the main answer to the question is option D, 1.489. We arrived at this answer by finding the derivative of the function g(x), setting it equal to zero, and testing the values of g(x) at the critical points and endpoints of the interval.
To learn more about derivative visit:
https://brainly.com/question/25324584
#SPJ11
12. use summation (õ) or product (œ) notation to rewrite the following.(a) 2 4 6 8 ··· 2n.(b) 1 5 9 13 ··· 425.(c) 1 12 13 14 ··· 150 .
Answers
Hello! I'm happy to help you with your question. Here's the notation for each sequence:
(a) 2 + 4 + 6 + 8 + ... + 2n can be rewritten as:
∑(2i) where i goes from 1 to n.
(b) 1 + 5 + 9 + 13 + ... + 425 can be rewritten as:
∑(4j-3) where j goes from 1 to 106. (Note: 425 is the 106th term in this sequence)
(c) 1 + 12 + 13 + 14 + ... + 150 can be rewritten as:
1 + ∑(k) ,where k goes from 12 to 150
Know more about summation notation
https://brainly.com/question/31366683
#SPJ11
Researchers once surveyed college students on their Fb use. The following two-way table displays data for the sample of students who responded to the survey.
Approximately what percent of students in the sample do not use Fb?
Round your answer to the nearest percent.
Answers
32% of students in the sample do not use Fac/ebook.
How to find the percentage of the students not using fac/ebookThe percentage of the students not using Faceb/ook is solved using the formula
= (number of students not using fa/cebook) / (total number of students) * 100
The number of students who do not use Fa/cebook is the sum of the values in the "Does not use Fac/ebook" column, which is 4 + 67 = 71.
The total number of students in the sample is the sum of the values in the "TOTAL" row, which is 219.
hence we have that
(71 / 219) × 100 ≈ 32.42
Rounding to the nearest percent approximately 32% of students in the sample do not use Fa/cebook.
Learn more about percentage at
https://brainly.com/question/24877689
#SPJ1
The graphs below show the test scores for students in different subject areas and the time the students spent studying
for the tests.
Math Scores vs. Hours Spent Studying
100 x
8882889822
Test Score
90-
80
70
60
50
40
30
20-
10-
0.5 1 1.5 2 2.5 3 3.5 4 4.5
Hours Spent Studying
Spelling Scores vs. Hours Spent Studying
Science Scores vs. Hours Spent Studying
100 I
90
Test Score
888888888
80
70
60
50
40
30
20-
10
0.5 1 1.5 2 2.5 3 3.5 4 4.5
Hours Spent Studying
History Scores vs. Hours Spent Studying
Save and Exit
Next
Submit
Answers
Answer:
The area of one side of a cuboid is 360cm. What is the length, if the width is 1.5cm?
if you have 18 dimes and
Quaters that are worth
2.25, which system would
represent this
Answers
The correct expression is,
⇒ $1.8 + 0.25y = $2.25
Where, y is number of quarters.
We have to given that;
You have 18 dimes and Quarters that are worth $2.25.
Since, We know that;
1 dimes = 0.10 dollar
1 quarters = 0.25 dollar
Hence, We get;
18 dimes = 18 x 0.10
= 1.8 dollars
So, We can formulate the correct expression which represent the situation is,
⇒ $1.8 + 0.25y = $2.25
Where, y is number of quarters.
Learn more about the measurement unit visit:
https://brainly.com/question/777464
#SPJ1
Suppose f is increasing on the interval [a, b] and we want to estimate the area under the curve on this interval. 1. If f is concave down on this interval, using left endpoints would give
Answers
If f is increasing on the interval [a, b] and concave down, using left endpoints to estimate the area under the curve would give an overestimate of the actual area.
To see why, consider dividing the interval [a, b] into n subintervals of equal width Δx = (b-a)/n. Let x0 = a, x1 = a + Δx, x2 = a + 2Δx, ..., xn = b be the endpoints of these subintervals. Then, the left endpoints approximation to the area under the curve is given by the Riemann sum:
R_n = Δx[f(x0) + f(x1) + f(x2) + ... + f(x(n-1))]
Since f is increasing, f(x0) ≤ f(x1) ≤ f(x2) ≤ ... ≤ f(x(n-1)) ≤ f(xn). Since f is concave down, its graph is below any secant line connecting two of its points. Therefore, the Riemann sum using left endpoints overestimates the area of the region under the curve, because the rectangles defined by the left endpoints have height f(x0), f(x1), ..., f(x(n-1)) and their top sides are above the curve.In contrast, using right endpoints to estimate the area would give an underestimate, because the rectangles would have their bottom sides above the curve.Therefore, the best approximation using rectangles would be the midpoint Riemann sum, which uses the midpoint of each subinterval as the height of the rectangle. This approximation is always between the left and right endpoint approximations and is closer to the actual area under the curve.
To learn more about “rectangles” refer to the https://brainly.com/question/25292087
#SPJ11
4.2. use the fourier transform analysis equation (4.9) to calculate the fourier transforms of: (a) b(t 1) b(t- 1) (b) fr{u( -2- t) u(t- 2)}
Answers
(a) the Fourier transform of b(t+1) b(t-1) is the square of the Fourier transform of b(t).
(a) Let's use the Fourier transform analysis equation (4.9) to find the Fourier transform of b(t+1) b(t-1):
F{b(t+1) b(t-1)} = ∫₋∞^∞ b(t+1) b(t-1) e₋ⱼωt dt
Let's make a substitution to simplify the expression:
u = t + 1, du = dt
v = t - 1, dv = dt
t = (u + v) / 2
dt = (du + dv) / 2
Substituting, we get:
F{b(t+1) b(t-1)} = ∫₋∞^∞ b(u) b(v) e₋ⱼω[(u+v)/2] (du+dv)/2
= 1/2 ∫₋∞^∞ [b(u) e₋ⱼωu] [b(v) e₋ⱼωv] e₋ⱼωu/2 e₋ⱼωv/2 du dv
= 1/2 ∫₋∞^∞ [b(u) e₋ⱼωu/2] [b(v) e₋ⱼωv/2] e₋ⱼω(u+v)/2 du dv
= 1/2 ∫₋∞^∞ [b(u) e₋ⱼωu/2] e₋ⱼωu/2 du ∫₋∞^∞ [b(v) e₋ⱼωv/2] e₋ⱼωv/2 dv
= [F{b(t)}]²
(b) Let's use the Fourier transform analysis equation (4.9) to find the Fourier transform of u(-2-t) u(t-2):
F{u(-2-t) u(t-2)} = ∫₋∞^∞ u(-2-t) u(t-2) e₋ⱼωt dt
Note that u(-2-t) is equal to 1 for t ≤ -2 and 0 otherwise, while u(t-2) is equal to 1 for t ≥ 2 and 0 otherwise. Therefore, the product u(-2-t) u(t-2) is equal to 1 for t between -2 and 2, and 0 otherwise. Using this information, we can write:
F{u(-2-t) u(t-2)} = ∫₋₂^₂ e₋ⱼωt dt
Integrating, we get:
F{u(-2-t) u(t-2)} = [e₋ⱼωt / ⱼω]₋₂^₂ = [e₋ⱼ2ω - e₋ⱼ(-2ω)] / ⱼω
Simplifying, we get:
F{u(-2-t) u(t-2)} = (sin(2ω) / ω) e₋ⱼω
Therefore, the Fourier transform of u(-2-t) u(t-2) is (sin(2ω) / ω) e₋ⱼω.
To learn more about Fourier transform visit:
brainly.com/question/29063535
#SPJ11